Recently NIAOT researcher team lead by Dr. Yi Zheng studied the data expression method on spherical cap. Three sets of orthogonal and complete functions are acquired with analytical form.
Complete orthogonal functions on spherical cap is an essential tool in many attractive researches: (a) in high aperture system like microscopy, lithography and data storage, it serves as an appropriate expansion base for aberration study; (b) it plays an important role in illumination design where lenses are routinely created to capture an entire hemisphere of light emitted from a source. (c) for real-time high-quality rendering, bidirectional reflectance distribution function defined on hemisphere is applied to characterize the incident and outgoing radiances. Accurately and efficiently representing it by a set of functions becomes particularly important; (d) human corneal is measured by video keratography, providing several thousand samples. Accurate modelling these data to a surface will serve to evaluation the overall image quality of eye, corneal refractive surgery and contact lens design; (e) functions on spherical cap are also extensively used in geomagnetic field study over a portion of the earth and cosmic microwave background research after removal galactic emission.
Functions on spherical cap has been of interest for a long time. Traditional planar functions involve a flat surface approximation that becomes less accurate as the coverage analyzed become curved. One prevalent approach is spherical harmonics. It loses orthogonality on the incomplete sphere and its redundancy cannot provide a stable fitting process. Even using their improved approaches, like regularization method, non-integral degree spherical function, are complicated and ill conditioned that limited their usage.
Yi’s team starts form the fact that spherical cap and planar circle are topological isomorphic. Therefore, map functions can be constructed between them. A simple and systematic process to derive Zernike like functions that are applicable to spherical cap is developed. And three function sets are acquired by Gram-Schmidt method. The first is hemispherical harmonics. It not only composes an orthogonal and complete set on hemisphere, but also reveal the connection between Zernike polynomials on circular plane and spherical harmonics on full sphere. The second is Zernike spherical function (ZSF) and the third is longitudinal spherical function (LSF). ZSF and LSF can be applied to arbitrary spherical cap and their orthogonality is invariant to aperture. The fit ability of obtained functions is also studied compared with spherical harmonics and Zernike polynomials. The research is published on Optics Express (Vol. 27, No. 26 37180–37195, 2019). Reviewers gives high evaluation on the study: I think that the research is important, as everyone knows how important orthonormal basis are in the description of physical processes. This method, in the case where the authors insist more on how the calculation should be done and present a clearer mathematical definition, is an important work for the community. This paper gives a way to everyone interested in fitting data from spherical cap to have access to an orthonormal basis. In my opinion, it does impact the fields where this fitting is needed.
The work is supported by National Natural Science Foundation of China (11190011, 11973008); Natural Science Foundation of Jiangsu Province (BK20141516).

Fig. 1. Hemispherical harmonics demonstration and its relationship with spherical harmonics. (a) Isometric plot for the first 15 hemispherical harmonics. (b) Filling lattice of HSH in SH diagram. Yellow blocks occupied by hemispherical harmonics and grey by complementary hemispherical harmonics.
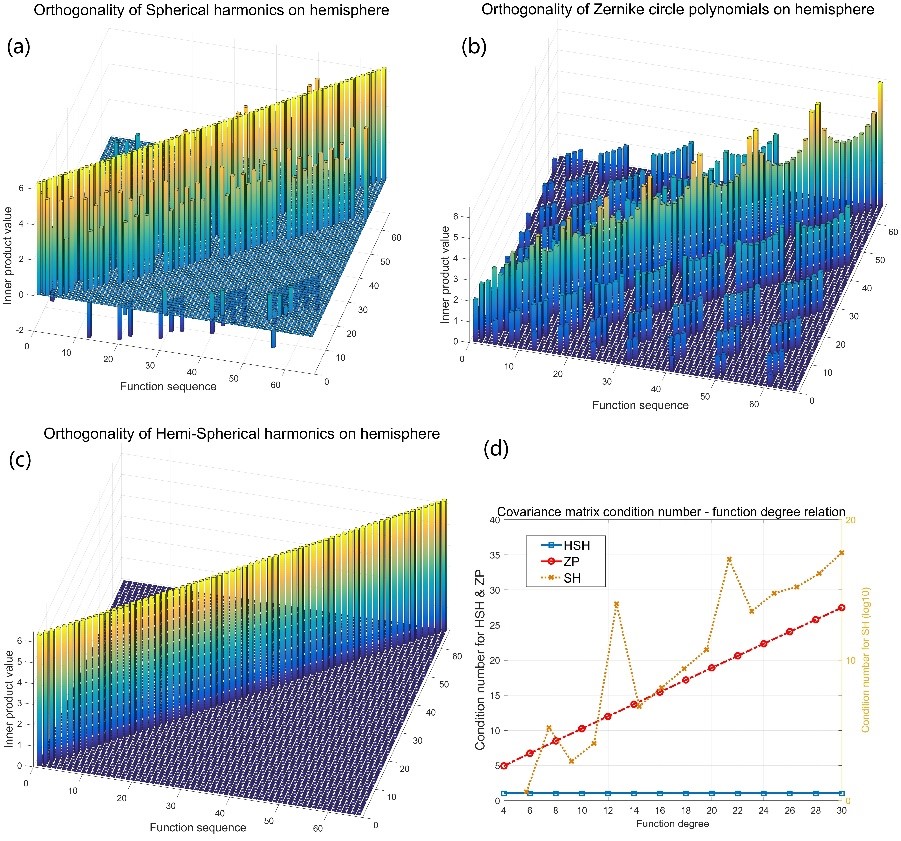
Fig. 2. Covariance matrix on hemi-sphere and condition number analysis. First 66 functions are taken out for demonstration. X and Y represent function sequence and Z axis is inner product value of two assigned function on hemisphere. (a) Covariance matrix for SH. (b) Covariance matrix for ZCP. (c) Covariance matrix for HSH. (d) Condition number with function degree. The magnitude of for HSH and ZCP is referenced to left Y axis and SH to the right log 10 axis.

Fig. 3. Fitting demonstration of HSH for step function on hemisphere. (a) Meridian section of fitting curves for 4, 20, 140-degree HSH with overhead view respectively on the right. (b) RMS residual fit error as function of the fit degree.